สวัสดีครับแฟนเพจที่รักทุกๆ ท่าน
กลับมาพบกันในทุกๆ วันพุธแบบนี้อีกครั้งหนึ่งซึ่งผมก็จะมาพบกับเพื่อนๆ เพื่อที่จะพูดคุยกันถึงหัวข้อ “ความรู้ดีๆ เรื่องประสบการณ์งานคำนวณออกแบบและการก่อสร้าง” นะครับ
เมื่อประมาณ 2 ถึง 3 สัปดาห์ก่อนหน้านี้มีรุ่นน้องวิศวกรท่านหนึ่งได้แจ้งกับผมมาว่า เค้าอยากจะให้ผมอธิบายถึงเรื่องหลักการของ FINITE ELEMENT ANALYSIS หรือที่เรานิยมเรียกกันสั้นๆ ว่า FEA สักหน่อย ซึ่งผมก็สาว่าเหมือนได้เคยเขียนเอาไว้บ้างเหมือนกันนะ ผมก็เลยไปลองรื้อๆ ดู ในที่สุดก็ไปเจอกับโพสต์เก่าที่ผมเขียนเอาไว้เมื่อประมาณ 2 ปีที่แล้ว ซึ่งตอนนั้นผมเคยเขียนเพื่อเป็นการอธิบายถึงเรื่อง การวิเคราะห์โครงสร้างด้วยวิธีเมตริกซ์ หรือ MATRIX ANALYSIS METHOD ให้กับเพื่อนๆ ไปแต่ไม่เป็นไร ผมจะขออนุญาตนำเอาโพสต์ๆ นั้นมาทวนซ้ำกันอีกสักหนึ่งรอบก็คงจะไม่เป็นการเสียหายอะไรนักนะครับ
วิธีการวิเคราะห์โครงสร้างด้วยวิธีการนี้ถือได้ว่าเป็นวิธีในการวิเคราะห์โครงสร้างที่มีความทันสมัย หรือ ADVANCED STRUCTURAL ANALYSIS METHOD วิธีการหนึ่งโดยวิธีการนี้ก็คือ วิธีการวิเคราะห์ด้วยเมตริกซ์ ซึ่งเป็นวิธีการที่ได้รับการพัฒนาและต่อยอดมาจากการอาศัยหลักการทางด้าน FINITE ELEMENT ANALYSIS นั่นเองครับ
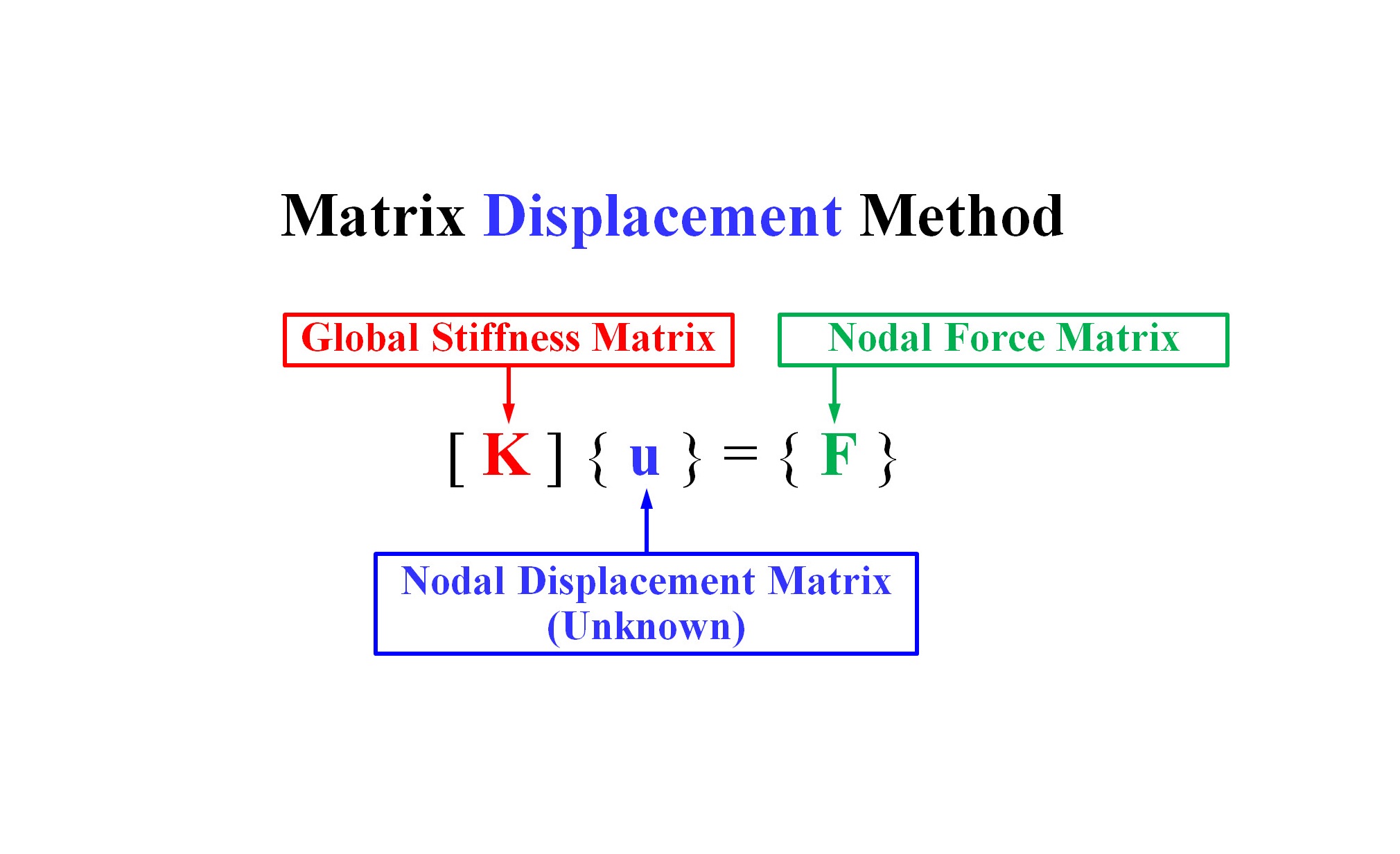
อย่างที่ผมได้เรียนเพื่อนๆ ไปก่อนหน้านี้ว่าวิธีการ MATRIX DISPLACEMENT METHOD นั้นจะได้รับความนิยมมากกว่าวิธีการ MATRIX FORCE METHOD ดังนั้นในวันนี้ผมจะขอเริ่มต้นอธิบายถึงขั้นตอนโดยสังเขปคร่าวๆ ของการวิเคราะห์โครงสร้างโดยวิธีการ MATRIX DISPLACEMENT METHOD และหากมีเวลาเหลือจริงๆ ผมก็จะขออนุญาตย้อนมาพูดถึงเรื่องวิธีการ MATRIX FORCE METHOD เพื่อที่เพื่อนๆ ทุกคนจะได้มีความรู้พื้นฐานของวิธีการๆ นี้ติดตัวเอาไว้บ้าง เผื่อเอาไว้ว่าเพื่อนๆ อาจจะมีโอกาสได้นำไปใช้งานในกรณีใดกรณีหนึ่งนั่นเอง ซึ่งรายละเอียดของขั้นตอนต่างๆ ในการวิเคราะห์โครงสร้างด้วยวิธีการ MATRIX DISPLACEMENT METHOD
นั้นจะประกอบไปด้วยขั้นตอนหลักๆ ทั้งหมด 11 ขั้นตอนดังต่อไปนี้ครับ
1. เริ่มต้นโดยการที่เราจะทำการกำหนดหมายเลขของ จุดต่อ หรือ NODE และ ชิ้นส่วน หรือ ELEMENT ที่มีอยู่ภายในระบบโครงสร้างเสียก่อน ทั้งนี้ก็เพื่อที่จะได้สามารถอ้างอิงถึงได้อย่างถูกต้องและเพื่อไม่เกิดความสับสนนะครับ
2. เราจะต้องทำการสร้างเมตริกซ์ที่มีความสำคัญมากตัวหนึ่งขึ้นมาก่อนนั่นก็คือ เมตริกซ์ความแข็งแกร่ง ของ ชิ้นส่วน ที่อ้างอิงตามแกนของ ชิ้นส่วนของโครงสร้าง หรือ MEMBER STIFFNESS MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [km] โดยหากเพื่อนๆ ติดตามมาโดยตลอดก็น่าที่จะจำได้ว่าผมเคยอธิบายถึงเรื่องๆ นี้ไปบ้างพอสังเขปก่อนหน้านี้แล้ว ยังไงหากเพื่อนๆ สนใจสามารถที่จะไปลองหาคลิปย้อนหลังดูกันได้นะครับ
3. เราจะใช้ความสัมพันธ์ของค่า แรง หรือ FORCE และ การเปลี่ยนตำแหน่ง หรือ DEFORMATION เพื่อที่จะทำการคำนวณหาความสัมพันธ์ระหว่างค่า แรงภายใน ที่เกิดขึ้นในชิ้นส่วนของโครงสร้าง ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ {f} กับค่า การเปลี่ยนแปลงรูปร่างของชิ้นส่วนโครงสร้าง ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ {d} ทั้งนี้หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ {d} นั้นเราจะทำการกำหนดให้ผลต่างๆ ของโครงสร้างนั้นอาศัย ระบบแกนอ้างอิงของชิ้นส่วนของโครงสร้าง หรือ LOCAL COORDINATE SYSTEM ซึ่งเราอาจจะสามารถเรียกกระบวนการนี้ได้ว่าเป็น FORCE-DISPLACEMENT RELATIONSHIP โดยในที่สุดเราก็อาจจะสามารถเขียนความสัมพันธ์ต่างๆ เหล่านี้ให้อยู่ในรูปแบบสมการเมตริกซ์อย่างเป็นทางการได้ว่า
{f} = [km] {d}
4. เราจะใช้ สมการความสอดคล้อง หรือ COMPATIBILTY EQUATION หรือ เงื่อนไขของความสอดคล้อง หรือ COMPATIBILTY CONDITION เพื่อที่จะเขียนความสัมพันธ์ของการเปลี่ยนแปลงรูปร่างของชิ้นส่วนโครงสร้าง {d} กับ การเปลี่ยนตำแหน่งที่จุดต่อ หรือ NODAL DISPLACEMENT ของชิ้นส่วนของโครงสร้าง {D} ทั้งนี้หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ {D} นั้นเราจะทำการกำหนดให้ผลต่างๆ ของโครงสร้างนั้นอาศัย ระบบแกนอ้างอิงของระบบของโครงสร้าง หรือ GLOBAL COORDINATE SYSTEM ทั้งนี้เราก็จะทำให้เราได้เมตริกซ์เพิ่มขึ้นมาอีกเมตริกซ์หนึ่งที่มีความสำคัญนั่นก็คือ เมตริกซ์แปลงค่าการเสียรูป หรือ DISPLACEMENT TRANSFORMATION MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [T] โดยในที่สุดเราก็อาจจะสามารถเขียนความสัมพันธ์ต่างๆ เหล่านี้ให้อยู่ในรูปแบบสมการเมตริกซ์อย่างเป็นทางการได้ว่า
{d} = [T] {D}
5. เราจะอาศัยสมการความสมดุลที่จุดต่อหรือ NODAL EQUILIBRIUM EQUATION เพื่อหาความสัมพันธ์ระหว่างแรงกระทำ {F} ทั้งนี้หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ {F} นั้นเราจะทำการกำหนดให้ผลต่างๆ ของโครงสร้างนั้นอาศัย ระบบแกนอ้างอิงของระบบของโครงสร้าง หรือ GLOBAL COORDINATE SYSTEM กับค่าแรงภายในที่เกิดขึ้นในชิ้นส่วนของโครงสร้าง {f} ที่เราได้หาไว้ก่อนหน้านี้แล้ว โดยในที่สุดเราก็อาจจะสามารถเขียนความสัมพันธ์ต่างๆ เหล่านี้ให้อยู่ในรูปแบบสมการเมตริกซ์อย่างเป็นทางการได้ว่า
{F} = [T]^(T) {f}
หมายเหตุไว้ตรงนี้ด้วยนะครับว่าสำหรับเมตริกซ์ [T]^(T) ก็คือ เมตริกซ์แปลงแรง หรือ FORCE TRANSFORMATION MATRIX นะครับ
6. เราจะหาความสัมพันธ์ของ แรงภายใน ที่เกิดขึ้นภายในชิ้นส่วนต่างๆ ของโครงสร้างกับค่าต่างๆ ของ การเปลี่ยนตำแหน่งที่จุดต่อ ดังนั้นเราก็จะสามารถทำได้โดยการแทนค่าเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 3 ซึ่งจะมีค่าเท่ากับ
{f} = [km] {d}
เข้าไปด้วยเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 4
{d} = [T] {D}
ดังนั้นก็จะได้ว่า
{f} = [km] [T] {D}
7. เราจะหาความสัมพันธ์ของ แรงภายนอก ที่เกิดขึ้นภายในระบบของโครงสร้างกับค่าต่างๆ ของ การเปลี่ยนตำแหน่งที่จุดต่อ ดังนั้นเราก็จะสามารถทำได้โดยการแทนค่าเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 5 ซึ่งจะมีค่าเท่ากับ
{F} = [T]^(T) {f}
เข้าไปด้วยเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 6
{f} = [km] [T] {D}
ดังนั้นก็จะได้ว่า
{F} = [T]^(T) [km] [T] {D}
8. ซึ่งตรงนี้เองที่เราจะสามารถสร้าง เมตริกซ์ความแข็งแกร่ง ของ ชิ้นส่วน ที่อ้างอิงตามแกนของ ระบบของโครงสร้าง หรือ STRUCTURAL GLOBAL STIFFNESS MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [k] ก็แล้วกัน ทั้งนี้ค่าเมตริกซ์ [k] นี้จะมีค่าเท่ากับ
[k] = [T]^(T) [km] [T]
ดังนั้นหากเราทำการแทนค่าเมตริกซ์ [k] ข้างต้นนี้ลงไปในเมตริกซ์ในข้อที่ 7 ก็จะทำให้ได้เมตริกซ์ของแรงภายนอกที่ถูกจัดรูปเสียใหม่ ซึ่งก็จะมีค่าเท่ากับ
{F} = [k] {D}
9. เราจะทำการจัดรูปและรวมเมตริกซ์ความแข็งแกร่งของโครงสร้างทั้งระบบออกมา ซึ่งในที่สุดก็จะได้ค่าเมตริกซ์ความแข็งแกร่งค่าสุดท้ายนั่นก็คือ เมตริกซ์ความแข็งแกร่ง ของ ระบบของโครงสร้าง หรือ STRUCTURAL STIFFNESS MATRIX ซึ่งในที่นี้ผมจะแทนให้อยู่อยู่ในรูปของเมตริกซ์ [K] ก็แล้วกัน ซึ่งพอทำการแทนลงไปในเมตริกซ์ที่เราได้สร้างเอาไว้ในข้อที่ 8 ก็จะได้เป็นเมตริกซ์ของแรงภายนอกของโครงสร้างทั้งระบบออกมาเป็นที่เรียบร้อยแล้วซึ่งก็จะมีค่าเท่ากับ
{F} = [K] {D}
10. ขั้นตอนนี้จะเป็นขั้นตอนของการหาคำตอบแล้ว โดยจะเริ่มต้นจากการจัดรูปเมตริกซ์ที่ได้ทำไว้ในข้อที่ 9 เพื่อที่จะใช้ทำการคำนวณหาค่า การเปลี่ยนตำแหน่งที่จุดต่อ ของโครงสร้างออกมาให้เราได้ทราบเสียก่อน ดังนั้นค่าเมตริกซ์ {D} ก็จะสามารถทำการคำนวณออกมาได้เท่ากับ
{D} = [K]^(-1) {Q}
11. ขั้นตอนนี้เป็นขั้นตอนสุดท้ายนั่นก็คือ เราจะทำการคำนวณหาค่าเมตริกซ์ {f} หรือ ค่าแรงภายในต่างๆ ของชิ้นส่วนต่างๆ ของโครงสร้างออกมา ดังนั้นเราก็จะทำการแทนค่าเมตริกซ์ {D} ที่หาได้จากในข้อที่ 10 ลงไปในเมตริกซ์ที่ได้สร้างเอาไว้ในข้อที่ 6 ซึ่งจะมีค่าเท่ากับ
{f} = [km] [T] {D}
เพียงเท่านี้ก็จะทำให้เราสามารถที่จะหาคำตอบของเมตริกซ์ {f} ซึ่งเป็นเมตริกซ์แรงภายในทั้งหมดของชิ้นส่วนโครงสร้างแล้วละครับ
ในครั้งต่อไปที่เราจะมาพบกัน ผมจะขออนุญาตมาทำการยกตัวอย่างถึงปัญหาสักหนึ่งข้อที่จะอาศัย MATRIX DISPALCEMENT METHOD เป็นวิธีในการที่เราจะทำการวิเคราะห์โครงสร้าง ทั้งนี้ก็เพื่อที่เพื่อนๆ ทุกคนจะได้นึกภาพวิธีในการทำตามที่ผมได้อธิบายด้วยคำพูดไปในโพสต์ๆ นี้ตามกันออก หากว่ามีเพื่อนๆ ท่านใดที่สนใจเป็นพิเศษในบทความๆ นี้ของผม ก็สามารถที่จะติดตามรับชมกันได้ในสัปดาห์หน้าครับ
ผมหวังว่าความรู้เล็กๆ น้อยๆ ที่ผมได้นำมาฝากแก่เพื่อนๆ ทุกๆ ท่านในวันนี้จะมีประโยชน์ต่อทุกๆ ท่านไม่มากก็น้อย และ จนกว่าจะพบกันใหม่นะครับ
#โพสต์ของวันพุธ
#ความรู้เรื่องประสบการณ์งานคำนวณออกแบบและการก่อสร้าง
#MatrixAnalysisOfStructure
#FEA
ADMIN JAMES DEAN
Bhumisiam (ภูมิสยาม)
บริษัท ภูมิสยาม ซัพพลาย จำกัด ผู้นำกลุ่มธุรกิจเสาเข็มสปันไมโครไพล์ รายแรกและรายเดียวในประเทศไทย ที่ได้การรับรองมาตรฐาน ISO 45001:2018 การจัดการอาชีวอนามัยและความปลอดภัย การให้บริการตอกเสาเข็ม The Provision of Pile Driving Service และได้รับการรับรอง ISO 9001:2015 ของระบบ UKAS และ NAC รายแรกและรายเดียวในประเทศไทย ที่ได้รับการรับรองระบบบริหารงานคุณภาพ ตามมาตรฐานในกระบวนการ การออกแบบเสาเข็มสปันไมโครไพล์ การผลิตเสาเข็มสปันไมโครไพล์ และบริการตอกเสาเข็มเสาเข็มสปันไมโครไพล์ (Design and Manufacturing of Spun Micropile/Micropile and Pile Driving Service)
บริษัท ภูมิสยาม ซัพพลาย จำกัด ได้รับการรับรองคุณภาพ Endoresed Brand จาก SCG ด้านการผลิตเสาเข็ม สปันไมโครไพล์ และได้รับเครื่องหมาย มาตรฐาน อุตสาหกรรม เสาเข็มสปันไมโครไพล์ Spun Micro Pile และเสาเข็มไอไมโครไพล์ I Micropile พร้อมรับประกันผลงาน และความเสียหายที่เกิดจากการติดตั้ง 7+ Year Warranty เสาเข็มมีรูกลมกลวงตรงกลาง การระบายดินทำได้ดี เมื่อตอกแล้วแรงสั่นสะเทือนน้อยมาก จึงไม่กระทบโครงสร้างเดิม หรือพื้นที่ข้างเคียง ไม่ต้องขนดินทิ้ง ตอกถึงชั้นดินดานได้ ด้วยเสาเข็มคุณภาพมาตรฐานเสาเข็มคอนกรีตเสริมเหล็กแบบแรงเหวี่ยง มอก.397-2562 และมาตรฐานเสาเข็มคอนกรีตเสริมเหล็กอัดแรงหล่อสำเร็จ มอก.396-2549 การผลิตที่ใช้เทคโนโลยีที่ทันสมัย จากประเทศเยอรมัน เสาเข็มสามารถทำงานในที่แคบได้ หน้างานสะอาด ไม่มีดินโคลน ทดสอบการรับน้ำหนักโดยวิธี Dynamic Load Test ด้วยคุณภาพและการบริการที่ได้มาตรฐาน เสาเข็มเราจึงเป็นที่นิยมในงานต่อเติม
รายการเสาเข็มภูมิสยาม
(การรับน้ำหนักขึ้นอยู่กับสภาพชั้นดินในแต่ละพื้นที่)
สอบถามเพิ่มเติมได้ 24ชม. ทุกวันค่ะ
☎️ 082-790-1447
☎️ 082-790-1448
☎️ 082-790-1449
☎️ 091-9478-945
☎️ 091-8954-269
📲 https://lin.ee/hum1ua2
📥 https://m.me/bhumisiam